 Problems on Techniques of Integration
Problems on Techniques of Integration Problems on Techniques of Integration
Problems on Techniques of Integration

We have
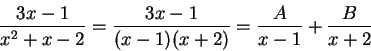
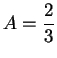 and
and
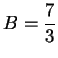 , or
, or
If you prefer to jump to the next problem, click on Next Problem below.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi