Problems on Techniques of Integration

The Arctangent function is one of these functions whose derivative is very nice (rational function). So it is a good idea to use the integration by parts technique in which $\arctan(x)$ will be differentiated. One may argue that we do not have two functions to apply this technique. That's true except that $\arctan(x)$ may also be seen as the product of the functions $1$ and $\arctan(x)$.

Set

$$\left\{\begin{array}{lll} u &=& \arctan(x)\\ dv &=& dx\;. \end{array}\right.$$

Then

$$\left\{\begin{array}{lll} du &=&\displaystyle \frac{1}{x^2 + 1} dx\\ v &=& x\;. \end{array}\right.$$

Since

$$\int u dv = u v - \int v du\;,$$

we get So

$$\int \arctan(x) dx = x \arctan(x) - \int x \frac{1}{x^2 + 1} dx = x \arctan(x) - \int \frac{x}{x^2 + 1}dx$$

But

$$\int \frac{x}{x^2 + 1}dx = \int \frac{1}{2}\; \frac{2x}{x^2 + 1}dx = \frac{1}{2} \ln(x^2+1)$$

which implies

$$\int \arctan(x) dx = x \arctan(x) - \frac{1}{2}\ln(x^2+1) + C\;.$$

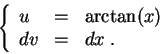
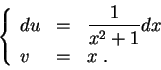
It is a common mistake to forget the constant $C$.

If you prefer to jump to the next problem, click on Next Problem below.

[Next Problem] [Matrix Algebra] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour