 Problems on Techniques of Integration
Problems on Techniques of Integration Problems on Techniques of Integration
Problems on Techniques of Integration

The Arctangent function is one of these functions whose derivative is very nice (rational function). So it is a good idea to use the integration by parts technique in which ![]() will be differentiated. One may argue that we do not have two functions to apply this technique. That's true except that
will be differentiated. One may argue that we do not have two functions to apply this technique. That's true except that ![]() may also be seen as the product of the functions
may also be seen as the product of the functions ![]() and
and ![]() .
.
Set
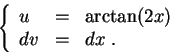
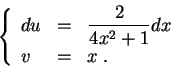
Since
It is a common mistake to forget the constant ![]() .
.
If you prefer to jump to the next problem, click on Next Problem below.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi