The Ratio Test
The Ratio TestLet's start by writing out the absolute ratios:
As in the previous example, we can simplify 
.
For the first term we want to use the hint, so let's rewrite
Do you feel like visiting our Algebra section? Just kidding...
Having jumped this hurdle, we can compute the limit of the ratios as
Thus the radius of convergence is 
, the series will converge in the interval from 
to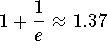 
.
Seeing is believing? Here are the pictures of the first terms of the power series:
|
|
|
|
|
|
|
|
|
|
Draw the graph of the power series on its interval of convergence. The behavior at the left is different from the behavior at the right. Try to explain the different behaviors!
