 More Problems on Sequences
More Problems on Sequences More Problems on Sequences
More Problems on Sequences

In this page you will find some not so easy problems on sequences. We invite you to solve them and submit the answer to SOS MATHematics. We will publish your answer with your name. Good luck.
Problem 1: Let ![]() be a sequence of real numbers such that
be a sequence of real numbers such that
![]() .
.
Show that
![]() .
.
A generalization of this result goes as follows:
![]() .
.
Then, we have
![]() .
.
Problem 2: Evaluate
![]() .
.
Problem 3: Discuss the convergence of
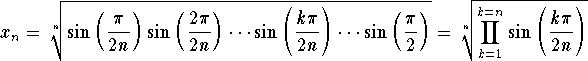 .
.
Problem 4: Discuss the convergence of
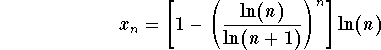 .
.
Problem 5: Let ![]() and
and ![]() be two sequences of
integers. Assume
be two sequences of
integers. Assume ![]() , for all
, for all ![]() , and
, and ![]() converges to an irrational number.
Show that
converges to an irrational number.
Show that
![]() .
.
Problem 6: Let ![]() (that is
(that is ![]() ). Show
that there exists a unique real number x such that
). Show
that there exists a unique real number x such that
![]() .
.
Call this number ![]() . Show that
. Show that
![]() .
.
Problem 7: Evaluate
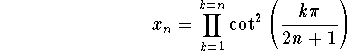 .
.
Use it to show that
![]() .
.
Problem 8: Let ![]() be a real number such that
be a real number such that ![]() . Set
. Set
![]() .
.
Find the limit of ![]() .
.
Problem 9: Let ![]() be a sequence of real numbers such that
be a sequence of real numbers such that
![]()
whenever ![]() . Assume that
. Assume that ![]() . Show that
. Show that
![]()
is convergent.
Problem 10: Let ![]() be a sequence of real numbers such that
be a sequence of real numbers such that
![]()
Show that the sequence
![]()
either converges to its lower bound or diverges to ![]() .
.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi