Taylor Polynomials
Taylor Polynomials
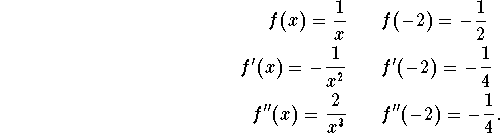
Using the formula above we obtain as the second degree Taylor polynomial:
No reason to only compute second degree Taylor polynomials!
If we want to find for example the fourth degree Taylor polynomial for a function f(x) with a given center 
, we will insist that the polynomial and f(x) have the same value and the same first four derivatives at .
A calculation similar to the previous one will yield the formula:
, where n indicates its degree.
(2) The factorial sign comes in handy:
Recall that 
. For instance 
Mathematicians usually say that 0!=1.
(3) Recall that one writes 
for the nth derivative of the functionf. 
just means f(x).
With these notations, we can then write the nth term of a Taylor polynomial as
Thus we obtain the general formula for the nth Taylor polynomial of a function f(x) with center :
An alternative way of writing this--for the not easily Mathematese-intimidated-- is provided by the summation notation:
with center 
.
Click here for the answer, or to continue.