Taylor Polynomials

Answer:

As you can see in the following animated picture for the example of this sine function, increasing the degree of the Taylor polynomial for a given function f(x) at a given point

generally has two effects:

At a given point x, the approximation of f(x) by the value of the Taylor polynomial 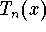becomes more accurate.
The approximation becomes ``good'' over a larger interval around the center . (This is really saying the same as the previous statement!)

The function sin(3x) is black, while its Taylor polynomials with center 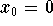are shown in red.

Click here if the animation does not work.

Try some more examples yourself!

Find the Taylor polynomial for the following functions and centers:

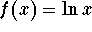, center , degree 5.
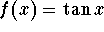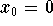, center , degree 3.
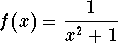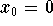, center , degree 3.

Click on a problem to see the answer. Click here to continue.

Helmut Knaust
Sun Jul 7 22:08:09 MDT 1996