Taylor Series

Since

displaymath79

its derivative has the Taylor expansion

displaymath80

The last step follows from the fact that

The hyperbolic functions differ from their trigonometric counterparts in that they do not sport alternating signs.

Taylor series and integration

Since integration is the inverse operation of differentiation, you should expect that it is also possible to integrate Taylor series term-by-term.

then its indefinite integral has the Taylor expansion

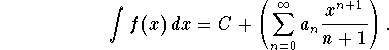
displaymath88

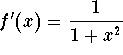Once again, this can be exploited to find Taylor series. Consider for instance the inverse tangent function . Its derivative is tex2html_wrap_inline99 , which has the Taylor series expansion

valid for -1<x<1. (This expansion can be found by using the geometric series!)

Consequently its integral has the Taylor series expansion

displaymath90

What is the appropriate choice for C? Plug in the center of the power series, in our case , on both sides of the equation:

so in this example C=0.

Integrating does not change the radius of convergence of a power series, so we expect the Taylor series expansion for the inverse tangent function to be valid for all -1<x<1.

Try it yourself!

Convince yourself that integration does not change the radius of convergence: Suppose the power series

has radius of convergence r. Show that its integral has radius of convergence r.

Click here for the answer, or to continue.

Helmut Knaust
Tue Jul 16 11:57:13 MDT 1996