| Answers. |
|---|
Problem 1. Evaluate
Answer. This is a definite integral. One way to handle it is to
find an antiderivative of 
and then
evaluate the result at 0 and 
.
Use integration by parts technique. Set
This gives
The technique of integrating rational functions gives
After easy calculations, we get
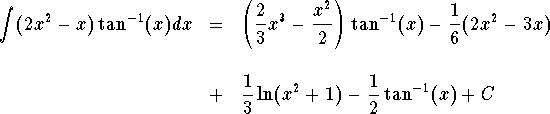
Now that we have the antiderivative we use it to get
Problem 2. Evaluate
Answer. We will use Substitution Techniques. Set
We have 
. The new integral is
The technique of integrating rational functions gives
Since
we have
Do not forget to go back to the variable x, we have
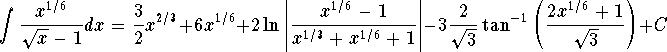
Problem 3. Evaluate
Answer. Note that this integral is direct from the formula
Indeed, if we let 
, then we have
in other words, we have
On the other hand, we may want to use the technique of integrating
rational functions of 
and 
. Let us show the main points
of this technique on this example for the sake of being somehow more
complete!!!
Set 
. Then we have
This gives
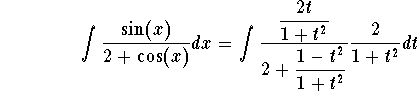
Easy algebraic computations yield:
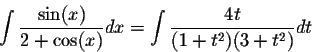
Since
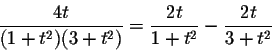
then we have
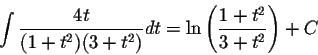
Back to the variable x, we have
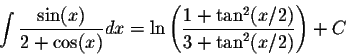
Using the half-angle formula for the cosine we obtain
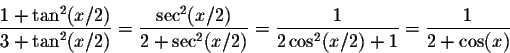
and thus finally
Problem 4. Evaluate
Answer. If we complete the square we get
which suggests the substitution 
. Hence 
. Therefore we have
Back to the variable x, we get
Problem 5. Evaluate
Answer. We have
We have
and
Putting the two together we get
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
