Differential Equations Practice Exams
Problem 1. Find the solution to:

Answer
Problem 2. Solve the initial value problem
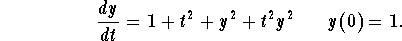
Answer
Problem 3. The fox squirrel is a small
mammal native to the Rocky Mountains. These squirrels are very
territorial:
- if the population is large, their rate of growth
decreases or even becomes negative;
- if the population is too small, fertile adults run the risk of
not being able to find suitable mates, so again the rate of growth is negative
The carrying capacity N indicates what population is too big, and
the sparsity parameter M indicates when the population is too small.
A mathematical model which will agree with the above assumptions is
the modified logistic model:
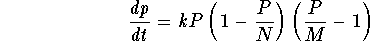
- 1.
- Find the equilibrium (critical) points. Classify them as :
source, sink or node. Justify your answers.
- 2.
- Sketch the slope-field.
- 3.
- Assume N=100 and M=1 and k = 1. Sketch the graph of the
solution which satisfies the initial condition y(0)=20.
- 4.
- Assume that squirrels are emigrating (from a certain region)
with a fixed rate E. Write down the new differential equation.
Discuss the equilibrium (critical) points under the parameter E.
When do you observe a bifurcation?
Answer
Problem 4. Consider the autonomous differential equation
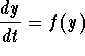 where the graph of f(y) is
where the graph of f(y) is
- 1.
- Sketch the Slope Fields of this differential equation
Hint: the graph of the solutions and the graph of f(y) are two different entities!
- 2.
- Sketch the graph of the solution to the IVP

Find the

- 3.
- Sketch the graph of the solution to the IVP
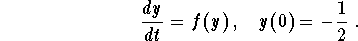
Find the

Answer
[Next Exam]
[Calculus]
[Differential equations]
[CyberExam]
 S.O.S MATH: Home Page
S.O.S MATH: Home Page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
![]()
![]()
![]()
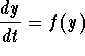 where the graph of f(y) is
where the graph of f(y) is
![]()
![]()
![]()
![]()
