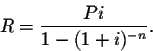Answer: The equation is y=-3x-1.
- (a) Find the break-even point.
Answer: The break-even point is 4 units.
- What revenue will the company receive if it sells just the
number of units from part (a)?
Answer: The revenue is $180.
- Find the profit function, P(x).
Answer: The profit function is P(x)=25x-100.
- Find the average cost per unit to produce 100 units.
Answer: The average cost per unit is $21.
Answer: The amount of money at the end will be about $441,739.
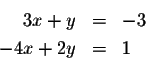
Answer:
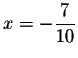 ,
,
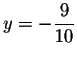 .
.
Answer:
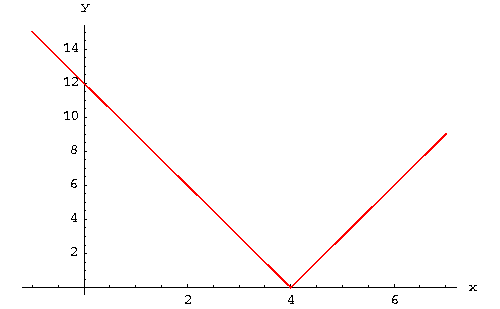
|
The x-intercept is 4, and the y-intercept is 12.
-
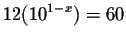 .
.
Answer: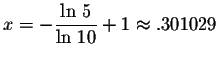 .
.
-
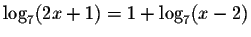
Answer: x=3.
- (a)
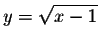 .
.
Answer: This represents a function. - (b) x=(y-1)2
Answer: This does not represent a function.
Answer: The first equation represents a function, because its graph passes
the vertical line test.
The second equation is not a function, because for many values of
x in the domain, there will be two different values for y in the
range, one positive and the other negative. This violates the
definition of a function.
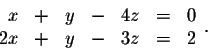
Answer: (Since there are only two equations and three unknowns,
the solutions will be parametrized in terms of one variable)
All solutions are given by (x, 8-5x, 2-x), where x is arbitrary. There are other parametrizations.
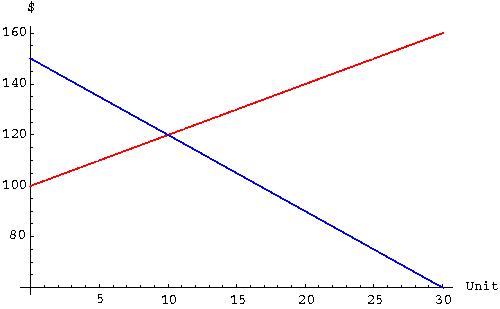 |
- At what price are 20 items supplied?
Answer: 20 items are supplied at $140.
- Find the equilibrium demand and the equilibrium price.
Answer: The equilibrium demand is 10 units, and the equilibrium price is $120 per unit.
- Are the supply and demand curves linear, quadratic, exponential,
logarithmic, or none of these?
Answer: The supply and demand curves are both linear.
Answer: The amount of each payment is $1,308.49.
- What is the domain of f(x).
Answer: The domain is all real numbers, or in interval notation,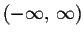 .
.
- Find any intercepts and asymptotes.
Answer: There is a horizontal asymptote at y=-1.
- Sketch the graph of f(x), including the intercepts and
asymptotes in your sketch.
Answer: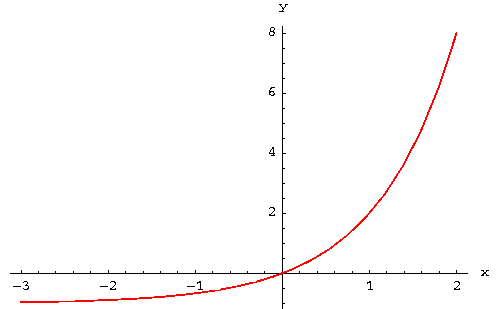
- If
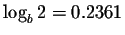 ,
,
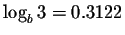 ,
and
,
and
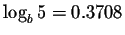 .
.
Find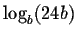 .
.
Answer: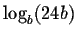 =
=
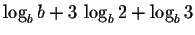 =2.0205.
=2.0205.
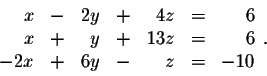
Answer:
![]() .
.
where t is time in hours since the patient was admitted, and y is the blood count.
- What was the patient's minimum blood count, and when did it
occur?
Answer: The patient's minimum blood count was 2,000, and it occurred 15 hours after admission.
- When the patient's blood count reached 3225, the patient was
discharged. When did this occur?
Answer: The patient's blood count reached 3223 and was discharged 50 hours after admission.
- Is the given equation linear, quadratic, exponential,
logarithmic, or none of these?
Answer: The given equation is quadratic.
Answer:
Let a= the number of blankets, b= the number of rugs and
let c= the number of skirts. The system of equations is:
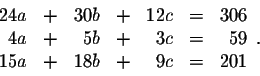
![$\displaystyle A=\left[\begin{array}{rr}
5&0\\
-1&3\\
4&7
\end{array}\right] $](img22.gif)
![$\displaystyle B=\left[\begin{array}{r}
6\\
1\\
0
\end{array}\right] $](img23.gif)
![$\displaystyle D=\left[\begin{array}{rr}
-1&4\\
3&7
\end{array}\right] $](img25.gif)
![$\displaystyle E=\left[\begin{array}{rr}
2&5\\
1&6
\end{array}\right] $](img26.gif)
- Give the dimensions of each matrix, and identify any square,
column, or row matrices.
Answer: The dimensions are: For A, 3 x 2. For B, 3 x 1, and the matrix is a column matrix. For C, 1 x 3, and the matrix is a row matrix. For D, 2 x 2, and the matrix is a square matrix. For E, 2 x 2, and the matrix is a square matrix.
- Find the following if possible:
- CA
Answer: [-14,-19],
- E-2D
Answer:![\begin{displaymath}\left[\begin{array}{rr}
4&-3\\
-5&-8
\end{array}\right].\end{displaymath}](img27.gif)
- BA
Answer: Not possible.
- CB
Answer: [9]
- CA
- Future value for simple interest:
A=P(1+rt).
- Future value for compound interest:
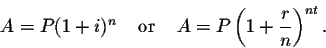
- Future value of an ordinary annuity:
![\begin{displaymath}S=\frac{R=[(1+i)^{n}-1]}{i}.\end{displaymath}](img30.gif)
- Future value of an annuity due:
![\begin{displaymath}S=\frac{R[(1+i)^{n+1}-1]}{i}-R.\end{displaymath}](img31.gif)
- Present value of an annuity:
![\begin{displaymath}P=\frac{R[1-(1+i)^{-n}]}{i}.\end{displaymath}](img32.gif)
- Amortizing a loan: