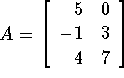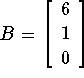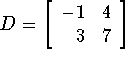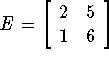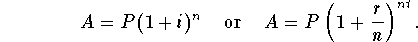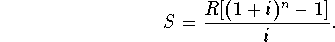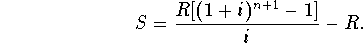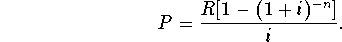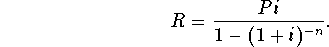- Find an equation for the line through the point (-2,5), which is
perpendicular to the line 3y-x+2=0.
- The cost of producing x units of a product is given by:
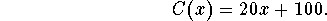
The product sells for $45 per unit.
- Find the break-even point.
- What revenue will the company receive if it sells just the
number of units from the part above?
- Find the profit function, P(x).
- Find the average cost per unit to produce 100 units.
- A 45-year old man puts $1,500 in a retirement account at the
end of the each quarter until he reaches the age of 60 and makes no
further deposits. If the account pays 12% interest compounded
quarterly, how much will be in the account when the man retires at age
65?
- Use the method of matrix inverses to solve the system of
equations

- Sketch the graph of f(x)=|3x-12|. Identify and include any
intercepts in your sketch.
- Solve each of the following for x:
- Which of the following (if any) represent y as a function of
x?
-
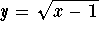 .
.
-
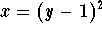 .
.
Explain your answers. That is, if you believe that the first expression is
(or is not) a function, explain how you came to this conclusion. Do
the same for the second expression. - Use the elimination method to solve the following system:
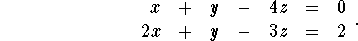
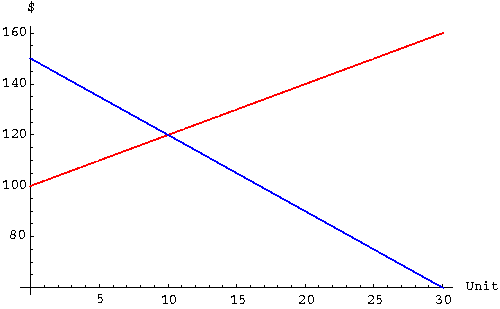
- Consider the supply and demand curves in the sketch below:
- At what price are 20 items supplied?
- Find the equilibrium demand and the equilibrium price.
- Are the supply and demand curves linear, quadratic, exponential,
logarithmic, or none of these?
(graph)
- A small resort must add a swimming pool to compete with a new
resort built nearby. The pool will cost $28,000. The resort borrows
the money and agrees to repay it in equal payments at the end of
each quarter for
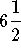 years at an interest rate of 6%
compounded quarterly. Find the amount of each payment.
years at an interest rate of 6%
compounded quarterly. Find the amount of each payment.
- Consider the function
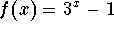 .
.
- What is the domain of f(x).
- Find any intercepts and asymptotes.
- Sketch the graph of f(x), including the intercepts and
asymptotes in your sketch.
- If
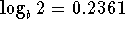 ,
, 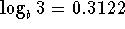 , and
, and
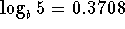 .
.
Find 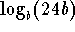 .
.
- Using the Gauss-Jordan method, solve the system of
equations:
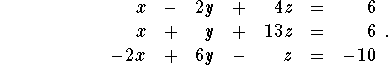
- A patient was admitted to a hospital with a declining white
blood cell count, described by the equation:
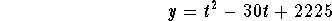
where t is time in hours since the patient was admitted, and y is
the blood count.
- What was the patient's minimum blood count, and when did it
occur?
- When the patient's blood count reached 3225, the patient was
discharged. When did this occur?
- Is the given equation linear, quadratic, exponential,
logarithmic, or none of these?
- The Waputi Indians make woven blankets, rugs, and skirts. Each
blanket requires 24 hrs for spinning the yarn, 4 hrs for dying the
yarn, and 15 hrs for weaving. Rugs require 30 hrs for spinning, 5 hrs
for dying, and 18 hrs for weaving. Skirts require 12 hrs for
spinning, 3 hrs for dying, and 9 hrs for weaving. There are 306 hours
available for spinning, 59 hrs for dying, and 201 hrs for weaving.
Set up a system of equations which could be used to determine the
number of blankets, rugs, and skirts made. Do not solve!
- Let
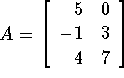
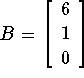
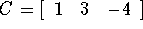
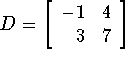
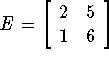
- Give the dimensions of each matrix, and identify any square,
column, or row matrices.
- Find the following if possible:
Formulas
- Future value for simple interest:

- Future value for compound interest:
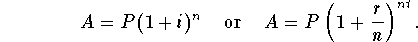
- Future value of an ordinary annuity:
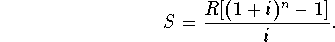
- Future value of an annuity due:
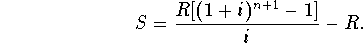
- Present value of an annuity:
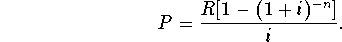
- Amortizing a loan:
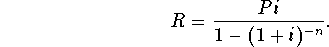
If you would like to check your answers, click on Answer.
If you would like to go back to the original menu, click on Menu.
Tue Aug 12 21:45:49 MDT 1997
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
![]()
![]()
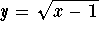 .
.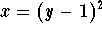 .
.![]()
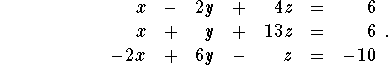
![]()