| Part 3
| Test 2
| Time: 3 hours
|
- Determine on what interval(s) the function
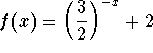 is decreasing.
is decreasing.
Answer:
d) 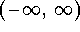 .
.
- Identify any asymptotes of the graph of
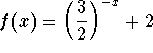 .
.
Answer:
a)
y=2.
- If you deposit $5,000 in a trust fund that pays 9.5% interest,
compounded continuously, which of the following values is closest to
the amount that will be in the trust after 50 years. Rounded to the
nearest $1.00.
Answer:
b) $577,921.
- The population model for a certain town is given by the equation
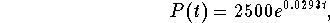
where t is the time in years, with t=0
corresponding to 1990. What will the population be in 2000?
Answer:
b) 3,351.
- Find the domain of the function
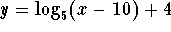 .
.
Answer:
a)
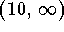 .
.
- Find the inverse function of the function
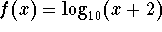 .
.
Answer:
b)
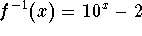 .
.
- Use the properties of logarithms to simplify the expression
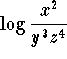 , and write as a sum difference,
and/or constant multiple of logarithms.
, and write as a sum difference,
and/or constant multiple of logarithms.
Answer:
d)
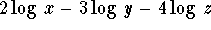 .
.
- Evaluate
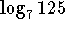 .
.
Answer:
a)
2.481262.
- Solve
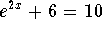 .
.
Answer:
d)
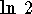 .
.
- Solve
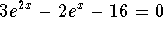 .
.
Answer:
b)
0.980829.
- Solve
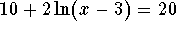 .
.
Answer:
c)
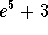 .
.
- Solve
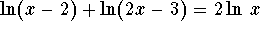 .
.
Answer:
c) None of the above, because only 6 is in the domain
of the original equation.
- The demand equation for a certain product is given by
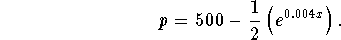
Find the demands x
for price 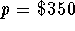 .
.
Answer:
a) 1426.
- How many years will it take your money to double if you deposit
it into a fund paying 10% compounded monthly?
Answer:
d) 6.96.
- How many years will it take your money to double if you deposit
it into an account paying 10% simple interest?
Answer:
a) 7.27.
- If the half-life of a substance is 500 years, how many years
will it take for 60% of the substance to disappear?
Answer:
c) 661.
- If bacteria is growing at the rate of 10 cells per second, how
long will it take for the culture to reach 1 million cells?
Answer:
d) 6 seconds.
- Which of the following is a power model?
Answer:
e) None of the above.
- Find the value of b in the exponential function
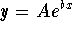 that passes through the points (0,2) and (4,3).
that passes through the points (0,2) and (4,3).
Answer:
c) 0.101366.
- Find the range of the function
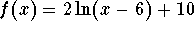 .
.
Answer:
b)
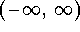 .
.
- Find the inverse of the function
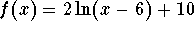 .
.
Answer:
d)
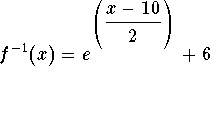 .
.
- Solve the following system of equations for x:

Answer:
e) None of the above. x = 2.
- Solve the following system of equations for y:

Answer:
c) 4.
- Find the value of b in the equation of the parabola
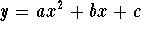 that passes through the points (0,6),
that passes through the points (0,6),
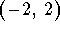 , and
, and 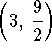 .
.
Answer:
a) 1.
- A small corporation borrowed $800,000 to expand its product
line. Some of the money was borrowed at 8%, some at 9%, and some at
10%. How much was borrowed at 9% if the annual interest was
$67,000 and the amount borrowed at 8% was five times the amount
borrowed at 10%.
Answer:
b) $50,000.
If you would like to practice on test out exams for Parts 1, 2 or 4, click on
Menu. It will take you back to the original menu.
Fri Oct 17 10:08:36 MDT 1997
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
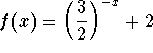 is decreasing.
is decreasing.
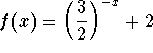 .
.
![]()
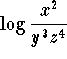 , and write as a sum difference,
and/or constant multiple of logarithms.
, and write as a sum difference,
and/or constant multiple of logarithms.![]()
![]() .
.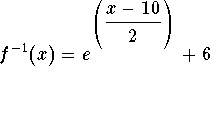 .
.
![]()

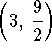 .
.