Answer: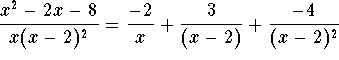 
.
Answer: The sequence is arithmetic, and the 
.
Answer: The sequence is geometric, and the sum equals
and 
.
- Find the formula which describes the nth term of this sequence.
Answer: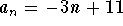
.
- Using the formula found above, write the first three terms
of the sequence.
Answer: The first three terms are 8, 5, 2.
Answer:
- When n=1, the formula is valid, because
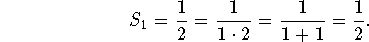
- Assuming that
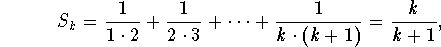
show that
To do this, write the following:
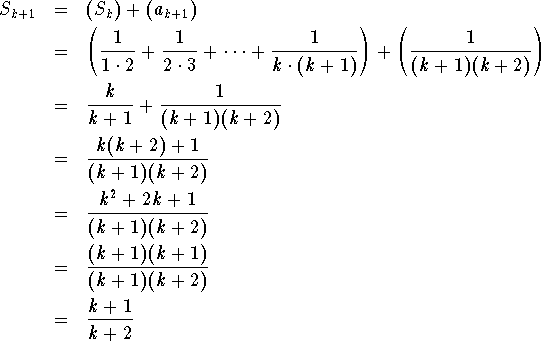
Combining the results of the two parts, it can be concluded by mathematical induction that the formula is valid for every positive integer n.
- Describe the sample space that considers the ordering of the
births of the 3 children.
Answer: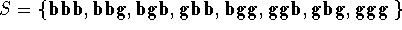
.
- Describe the event that the family has exactly 2 girls.
Answer: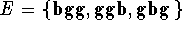
.
.
- Using the Binomial Theorem, write out the binomial expansion of
the given expression and compute the third binomial coefficient by
hand (show all steps).
Answer: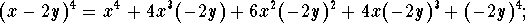
the third binomial coefficient is equal to 6.
- Using any method (calculator or by hand) find the rest of the
coefficients, and simplify the expansion in the above part.
Answer: Coefficients are: 1, 4, 6, 4, and 1, and simplification of the expression yields: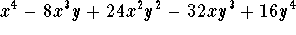
.
- In how many ways can she arrange them in a row if they are all
different colors?
Answer: In 14!=87,178,291,200 different ways. - In how many distinguishable ways can they be arranged in a row
if objects of the same shape are also the same color?
Answer: In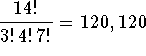
different ways.
Answer: 
or approximately 0.3077.
Answer: In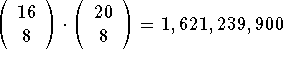 
different ways.