Linear Equations: Answer to Example 1

Example: Find the solution to

.

Solution: First, we recognize that this is a linear equation. Indeed, we have

Therefore, the integrating factor is given by

.

Since , we get

Hence, the general solution is given by the formula

We have

The details for this calculation involve the technique of integrating rational functions. We have

Hence, the only difficulty is in the integral 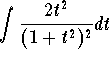. Here we will use integration by parts. We will differentiate t and integrate 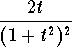. The details are left to the reader. We have

Therefore, we have

,

which clearly implies

The general solution can also be rewritten as

Finally, the initial condition y(0) = 0.4 gives C = 0.4. Therefore, the solution to the IVP is

Next Example.

[Differential Equations] [Linear Equations] [Separable Equations] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S. MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Last Update 6-22-98

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour