Separable Equations: Answer to Example 1

Example: Find all solutions to

.

Solution: First, we look for the constant solutions, that is, we look for the roots of

This equation does not have real roots. Therefore, we do not have constant solutions.

The next step will be to look for the non-constant solutions. We proceed by separating the two variables to get

.

Then we integrate

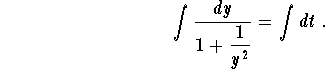
Since

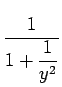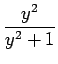$${\frac{{1}}{{1 + \displaystyle \frac{1}{y^2}}}}$$ = $${\frac{{y^2}}{{y^2+1}}}$$ = 1 - $${\frac{{1}}{{y^2+1}}}$$

we get

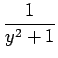
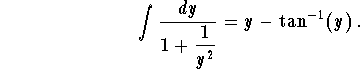
Therefore, we have

It is not easy to obtain y as a function of t, meaning finding y in an explicit form.

Finally, because there are no constant solutions, all the solutions are given by the implicit equation

Next Example.

[Differential Equations] [Linear Equations] [Next Example] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S. MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Last Update 6-22-98

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour