Method of Variation of Parameters
Method of Variation of Parameters
This method is interesting whenever the previous method does not apply (when g(x) is not of the desired form). The general idea is similar to what we did for second order linear equations except that, in that case, we were dealing with a small system and here we may be dealing with a bigger one (depending on the order of the differential equation). Let us describe the general case (constant coefficients or not). Consider the equation
Suppose that a set of independent solutions 
of the associated homogeneous equation is known. Then a particular
solution can be found as
where the functions 
can be obtained from the following system:
.
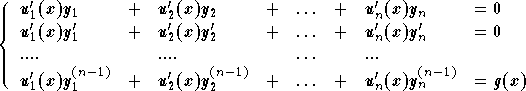The determinant of this system is the Wronskian of
, which is not zero. Cramer's formulas will give
,
where W(x) is the Wronskian 
and 
is the
determinant obtained from the Wronskian W by replacing the
-column in the vector column (0,0,..,0,1). Consequently,
a particular solution to the equation (NH) is given by
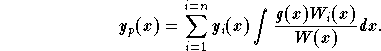
Note that when the order of the equation is not high, you may want to
solve the system using techniques other than Cramer's formulas.
Example: Find a particular solution of
Solution: Let us follow these steps:
Since 
, the roots of the characteristic equation
are 
. Therefore, a set of independent solutions is
;
, where 
are solutions of the system
;
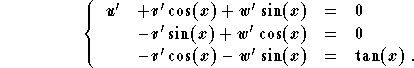After integration we get
;
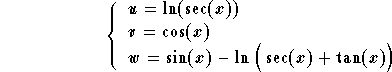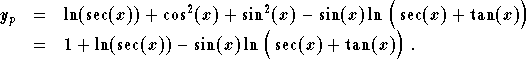
Note that the constant 1 in 
may be dropped since it is the
solution of the associated homogeneous equation.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Mohamed Amine Khamsi