 Introduction: Answer to Example4
Introduction: Answer to Example4

Example: Consider the following predator-prey model:
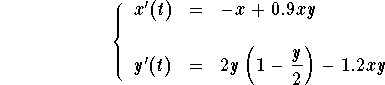 .
.
- 1.
- Does x(t) denote the predator population or the prey population? Justify your answer.
- 2.
- Find all equilibrium points of the system.
- 3.
- Suppose the prey population becomes extinct while the predator population is still positive. Describe the long-term behavior of the predator population.
- 4.
- Suppose the predator population becomes extinct while the prey population is still positive. Describe the long-term behavior of the prey population.
- 5.
- Describe the long-term behavior of the system when the initial populations are given by
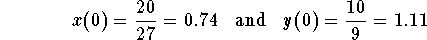 .
.
Answer:
- 1.
- Recall that in the absence of prey, the population of
predators decrease. It is clear that if y=0, then we have x'(t) = -x, meaning that x(t) will decrease. While, if we set x=0, we have y'=2y(1-y/2). Here we recognize the logistic equation which implies that y should get closer and closer to the carrying capacity y=2. Conclusion x represents the predator population.
-
2
- The equilibrium points are solutions of the system
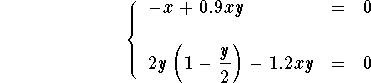 .
.
Since,
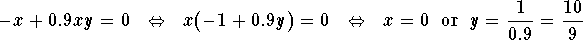 ,
,
we have the following two cases:
- Case 1: x=0, then the second equation gives
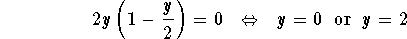 .
.
Hence, we have two equilibrium points
 .
.
- Case 2: y=10/9, then the second equation gives
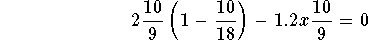 ,
,
which gives
 .
.
Hence, one equilibrium point (in this case)
 .
.
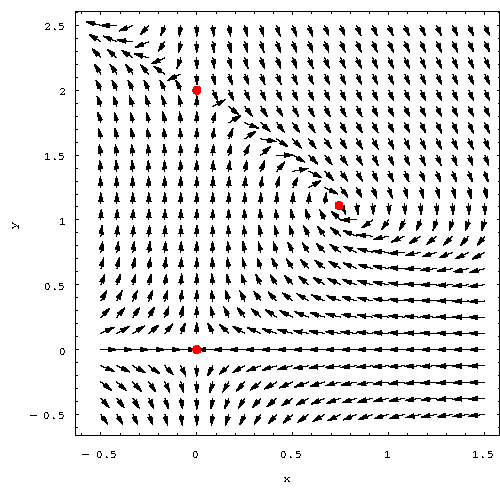
Finally, the system has three equilibrium points 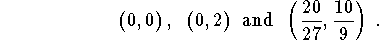
- 3.
- It will become extinct.
- 4.
- It will approach the carrying capacity y=2.
- 5.
- Using the answer to 2, we see that the initial populations correspond to an equilibrium point. Therefore, both populations will remain unchanged
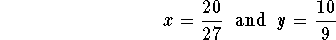 .
.
Next Example:

[Differential Equations]
[First Order D.E.]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard..

Author:
Mohamed Amine Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Introduction: Answer to Example4
Introduction: Answer to Example4 Introduction: Answer to Example4
Introduction: Answer to Example4
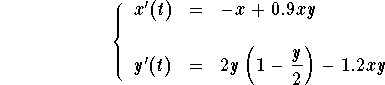 .
. ![]() .
. 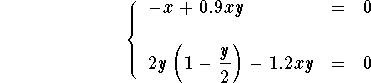 .
. ![]() ,
, ![]() .
. ![]() .
. ![]() ,
, ![]() .
. ![]() .
. ![]()

![]() .
. 
 S.O.S MATHematics home page
S.O.S MATHematics home page 