Answer to Example 5
Answer to Example 5
Example: Find the solution to the system
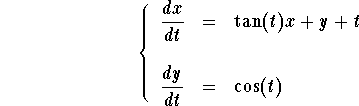
under the initial condition 
.
Answer: Notice that the second equation of the system is a differential equation involving only the variable y. Its integration gives
Note that 
is the derivative of 
not its anti-derivative! The initial condition translates into the initial condition y(0)=0 for the variable y. Hence, we have
,
which gives 
. Since we have y, we plug it into the first equation to get
We recognize a first order linear differential equation. In order to solve it, first we need to find the integrating factor given by
Note that the anti-derivative of 
is 
. The general solution is then given by
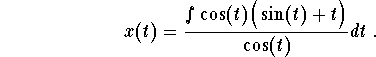
We have
,
and
,
where, in the first integral, we used direct tables and for the second one we used
integration by parts (we integrated and differentiated t). Putting everything together, we get
.
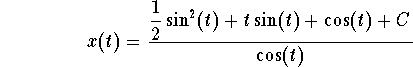The initial condition translates into the initial condition x(0)=1 for the variable x. Hence, we have
which gives C=0. Therefore, we have
.
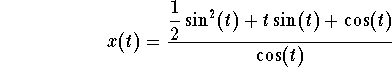Finally, the solution to the system is
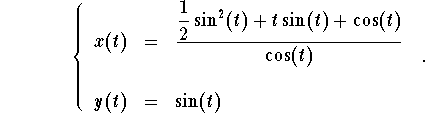
Note that since 
, we may generate another expression for the function x(t).
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard..
Author: Mohamed Amine Khamsi