Complex Eigenvalues: Example 1
Complex Eigenvalues: Example 1
Example: Solve the initial value problem
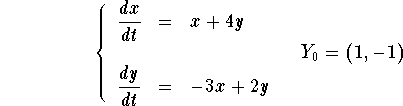
Answer: First, note that the matrix coefficient is
Next, we need to find the eigenvalues which are given as roots of the characteristic equation
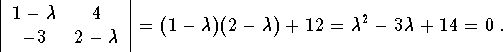
This is a quadratic equation. Its roots are given by the quadratic formulas
Set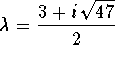 
, and find an associated eigenvector V. Set
The vector V must satisfy the equation
.
This is equivalent to the system
.
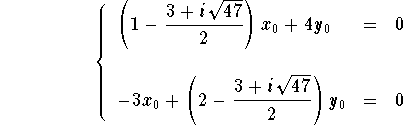From the quadratic equation we get (check it)
,
then we have
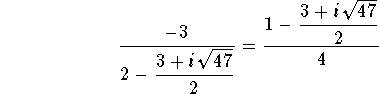
This clearly implies that the two equations of the system are the same. Therefore, we use only the first to get
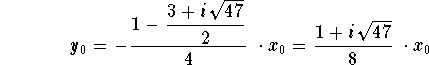
Hence, we have
Choose
The independent solutions which will generate the general solution to the system are the real and the imaginary parts of the complex solution
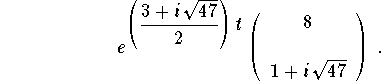
Since
,
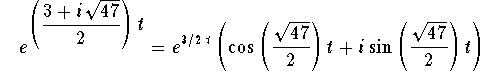and
,
where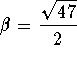 
, we have
,
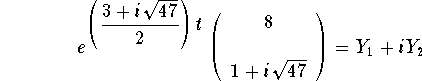where
,
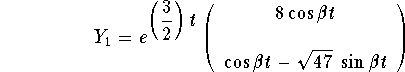and
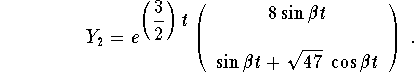
Therefore, the general solution is
The initial condition 
implies
,
which gives
Therefore, the desired particular solution is
,
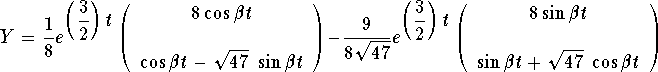where
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Mohamed Amine Khamsi