 Real Eigenvalues: Example1
Real Eigenvalues: Example1

Example: Consider the harmonic oscillator with spring constant 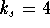 , damping constant
, damping constant 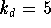 , and the mass m=1.
, and the mass m=1.
- (1)
- Write down the second order equation governing this physical system. Use the letter y for the spring's displacement from its rest position.
- (2)
- Convert this equation into a linear system of first order differential equations.
- (3)
- Solve the system.
- (4)
- Find the particular solution which satisfies the initial conditions
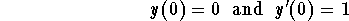
- (5)
- Discuss the long-term behavior of the system. Is this conclusion probable?
Solution:
Next Example:

[Differential Equations]
[First Order D.E.]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author:
Mohamed Amine Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Real Eigenvalues: Example1
Real Eigenvalues: Example1 Real Eigenvalues: Example1
Real Eigenvalues: Example1
![]() , damping constant
, damping constant ![]() , and the mass m=1.
, and the mass m=1.
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page 