Repeated Eigenvalues: Example1

Example. Consider the system

1.

Find the general solution.

2.

Find the solution which satisfies the initial condition

3.

Draw some solutions in the phase-plane including the solution found in 2.

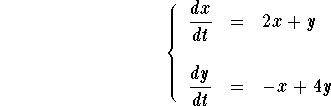
Answer. The matrix coefficient of the system is

In order to find the eigenvalues consider the characteristic polynomial

Since , we have a repeated eigenvalue equal to 3. Let us find the associated eigenvector . Set

Then we must have which translates into

This reduces to y=x. Hence we may take

Next we look for the second vector . The equation giving this vector is which translates into the algebraic system

where

Clearly the two equations reduce to the equation y - x=1 or y = 1 + x, where x may be chosen to be any number. So if we take x=0 for example, we get

Therefore the two independent solutions are

The general solution will then be

In order to find the solution which satisfies the initial condition

we must have

This implies and . Hence the solution is

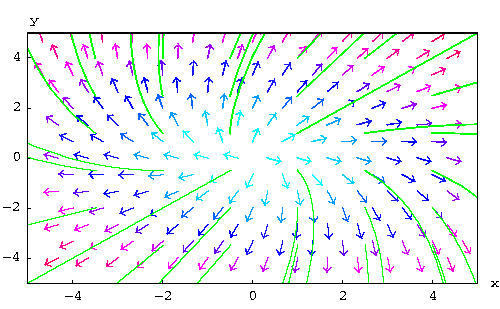
The phase plane with some solutions is given in the picture below:

[Differential Equations] [First Order D.E.] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour