 Answer
Answer

Assume that 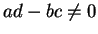 . Let us show that
. Let us show that  is row equivalent to
is row equivalent to  . Assume moreover that
. Assume moreover that 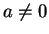 . Then divide the first row by
. Then divide the first row by 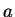 to get the new matrix
to get the new matrix
Now take the second row minus 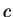 times the first row to get
times the first row to get
Divide the second row by
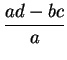 since it not equal to 0 to get
since it not equal to 0 to get
Finally take the first row minus
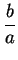 times the first row to get
times the first row to get
Our proof is almost complete, if we show that the conclusion still holds when 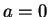 . In this case, neither
. In this case, neither 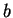 nor
nor 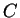 are equal to 0. Switch the first row with the second one to get
are equal to 0. Switch the first row with the second one to get
Divide the first row by 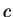 and the second row by
and the second row by 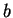 to get
to get
Take the first row minus
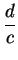 times the second row to get
times the second row to get
The proof is now complete.
Click on Next Problem below to go to the next problem.

[Next Problem]
[Matrix Algebra]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Calculus]
[Complex Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Answer
Answer Answer
Answer
![]() . Let us show that
. Let us show that ![]() is row equivalent to
is row equivalent to ![]() . Assume moreover that
. Assume moreover that ![]() . Then divide the first row by
. Then divide the first row by ![]() to get the new matrix
to get the new matrix
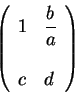
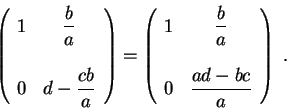
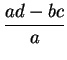 since it not equal to 0 to get
since it not equal to 0 to get
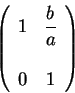
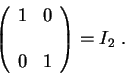
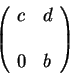
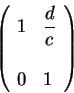
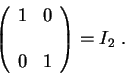

 S.O.S MATHematics home page
S.O.S MATHematics home page 