 More Problems on Linear Systems and Matrices
More Problems on Linear Systems and Matrices

Let us answer (1). Consider the augmented
matrix of the system
Let us do some row elementary operations. First take second Row
minus first row and third row minus 3 times first row, that is
to get
Next take
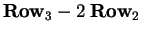 to get
to get
So the original system is consistent if and only if
Next we answer (2). If
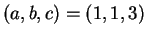 then we have
then we have
so the condition is satisfied. Therefore the system is
consistent.
If
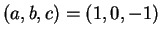 , then we have
, then we have
so the system in this case is not consistent.
Click on Next Problem below to go to the next problem.

[Next Problem]
[Matrix Algebra]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Calculus]
[Complex Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 More Problems on Linear Systems and Matrices
More Problems on Linear Systems and Matrices More Problems on Linear Systems and Matrices
More Problems on Linear Systems and Matrices
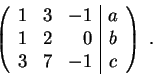
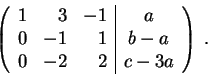
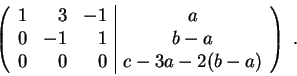
![]() then we have
then we have

 S.O.S MATHematics home page
S.O.S MATHematics home page 