 SYSTEMS OF EQUATIONS in TWO VARIABLES
SYSTEMS OF EQUATIONS in TWO VARIABLES SYSTEMS OF EQUATIONS in TWO VARIABLES
SYSTEMS OF EQUATIONS in TWO VARIABLES
A system of equations is a collection of two or more equations with the same set of unknowns. In solving a system of equations, we try to find values for each of the unknowns that will satisfy every equation in the system.
The equations in the system can be linear or non-linear. This tutorial
reviews systems of linear equations.
A problem can be expressed in narrative form or the problem can be expressed
in algebraic form.
Let's start with an example stated in narrative form. We'll convert it to an
equivalent equation in algebraic form, and then we will solve it several
ways.
Example 2:
How much of a 7% acid solution should be mixed with how much of a 15% acid
solution so that you obtain 20 gallons of a 12% acid solution?
A 7% acid solution means that 0.07 times the total solution is
acid.
Solution:
We have two unknowns: the amount of 7% acid solution and the amount of 15%
acid solution. Our objective is to find these two numbers.
The sentence essentially says that if we add a certain amount of the 7%
percent acid solution to a certain amount of the 15% acid solution, we
will have 20 gallons with a 12% acid solution. Let's restate this sentence
with two sentences.
Sentence (1):''The amount of the 7% acid solution'' + ''the amount of the
15% acid solution'' = 20 gallons.
Sentence (2): ''The amount of acid in the 7% acid solution'' + ''the amount
of acid in the 15% acid solution'' = 0.12(20) = 2.4 gallons.
It is going to get tiresome writing the two phrases (the amount of the 7%
acid solution) and (the amount of the 15% acid solution) over and over
again. So let's write them in shortcut form. Call the phrase (the amount of
7% acid solution) by the symbol ![]() and call the phrase (the amount of 15%
acid solution) by the symbol
and call the phrase (the amount of 15%
acid solution) by the symbol ![]() .
.
The amount of acid in the 7% acid solution can then be written as ![]() ,
and the amount of acid in the 15% acid solution can be written as
,
and the amount of acid in the 15% acid solution can be written as ![]() .
.
Let's rewrite sentences (1) and (2) in shortcut form.
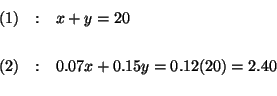
We have converted a narrative statement of the problem to an equivalent
algebraic statement of the problem. Let's solve this system of
equations.
A system of linear equations can be solved four different ways:
Substitution,
Elimination,
Matrices,
Graphing.
The Method of Substitution:
The method of substitution involves several steps:
Step 1:
Solve for y in equation (1).
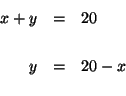
Step 2:
Substitute this value for y in equation (2). This will change equation (2)
to an equation with just one variable, x.
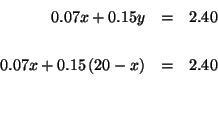
Step 3:
Solve for x in the translated equation (2).
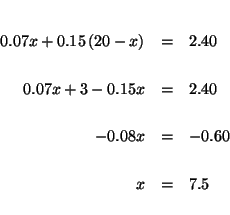
Step 4:
Substitute this value of x in equation (1) to solve for y.
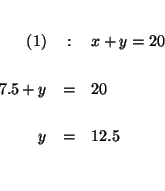
Step 5:
Check your answers by substituting the values of ![]() and
and ![]() in each of the
original equations. If, after the substitution, the left side of the
equation equals the right side of the equation, you know that your answers
are correct.
in each of the
original equations. If, after the substitution, the left side of the
equation equals the right side of the equation, you know that your answers
are correct.
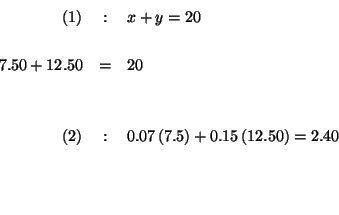
The process of substitution involves several steps:
In a two-variable problem rewrite the equations so that when the equations
are added, one of the variables is eliminated, and then solve for the
remaining variable.
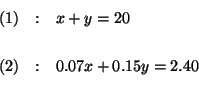
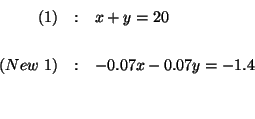
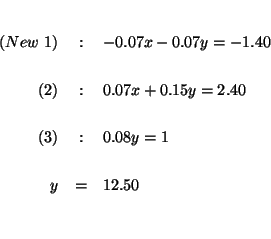
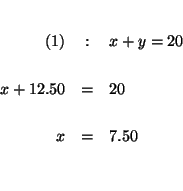
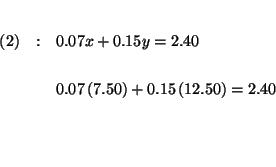
This method is essentially a shortcut for the method of elimination.
Rewrite equations (1) and (2) without the variables and operators. The left
column contains the coefficients of the x's, the middle column contains the
coefficients of the y's, and the right column contains the
constants.
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrrr...
...
& & & & \vert & & \\
0.07 & & 0.15 & & \vert & & 2.40
\end{array}
\right] $](img19.gif)
The objective is to reorganize the original matrix into one that looks like
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrrr...
...
& & & & \vert & & \\
0 & & 1 & & \vert & & b
\end{array}
\right] \bigskip $](img20.gif)
Step 1.
Manipulate the matrix so that the number in cell 11 (row 1-col 1) is 1. In
this case, we don't have to do anything. The number 1 is already in the
cell.
Step 2:
Manipulate the matrix so that the number in cell 21 is 0. To do this we
rewrite the matrix by keeping row 1 and creating a new row 2 by adding
![]() .
.
![\begin{eqnarray*}
&& \\
-0.07\left[ Row\ 1\right] +\left[ row\ 2\right] &=&\left[ New\ Row\
2\right] \\
&&
\end{eqnarray*}](img22.gif)
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrrr...
...0 \\
& & & & \vert & & \\
0 & & 0.08 & & \vert & & 1
\end{array}
\right] $](img23.gif)
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrrr...
... \\
& & & & \vert & & \\
0 & & 1 & & \vert & & 12.50
\end{array}
\right] $](img24.gif)
![\begin{eqnarray*}
&& \\
-1[Row\ 2]+[Row\ 1] &=&[New\ Row\ 1] \\
&&
\end{eqnarray*}](img25.gif)
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrrr...
... \\
& & & & \vert & & \\
0 & & 1 & & \vert & & 12.50
\end{array}
\right] $](img26.gif)
The method of Graphing:
In this method, solve for y in each equation and graph both. The point of
intersection is the solution.
If you would like to work a similar example, click on Example.
If you would like to test yourself by working some problem similar to this example, click on
Problem.
This site was built to accommodate the needs of students. The topics and problems are what
students ask for. We ask students to help in the editing so that future viewers will access
a cleaner site. If you feel that some of the material in this section is ambiguous or needs
more clarification, or if you find a mistake, please let us know by e-mail at sosmath.com.

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus