 SYSTEMS OF EQUATIONS in TWO VARIABLES
SYSTEMS OF EQUATIONS in TWO VARIABLES SYSTEMS OF EQUATIONS in TWO VARIABLES
SYSTEMS OF EQUATIONS in TWO VARIABLES
A system of equations is a collection of two or more equations with the same set of unknowns. In solving a system of equations, we try to find values for each of the unknowns that will satisfy every equation in the system.
The equations in the system can be linear or non-linear. This tutorial
reviews systems of linear equations.
A problem can be expressed in narrative form or the problem can be expressed
in algebraic form.
Let's start with an example stated in narrative form. We'll convert it to an
equivalent equation in algebraic form, and then we will solve it.
Example 6:
Two planes start from the same airport and fly in different directions. The
second plane starts one-half hour after the first plane, but its speed is 50
miles per hour faster. Find the ground speed of each plane if 2 hours after
the first plane starts the planes are 2000 miles apart.[Ground speed is the
speed of the plane discounting any wind.]
The distance the first plane traveled plus the difference the second plane
traveled totals 2000 miles. If we let the phrase ''distance the first plane
traveled'' be represented by the symbol ![]() and the phrase ''distance
the second plane traveled'' be represented by the symbol
and the phrase ''distance
the second plane traveled'' be represented by the symbol
![]() The sentence ''The distance the first plane traveled plus the difference the
second plane traveled totals 2000 miles.'' can be written as
The sentence ''The distance the first plane traveled plus the difference the
second plane traveled totals 2000 miles.'' can be written as
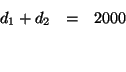
The distance the first plane traveled can now be represented by the equation
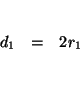
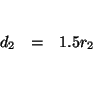
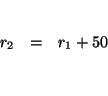
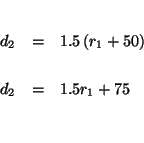
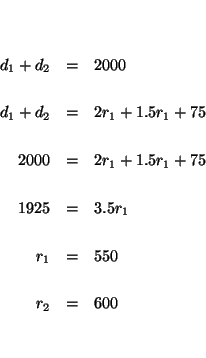
First Plane: speed ![]() time =
time =
![]() Second Plane: speed
Second Plane: speed ![]() time =
time =
![]() The sum of the distances is
The sum of the distances is
![]()
If you would like to test yourself by working some problem similar to this example, click on Problem.
This site was built to accommodate the needs of students. The topics and problems are what
students ask for. We ask students to help in the editing so that future viewers will access
a cleaner site. If you feel that some of the material in this section is ambiguous or needs
more clarification, or if you find a mistake, please let us know by e-mail at sosmath.com.

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus