 SYSTEMS OF EQUATIONS in TWO VARIABLES
SYSTEMS OF EQUATIONS in TWO VARIABLES SYSTEMS OF EQUATIONS in TWO VARIABLES
SYSTEMS OF EQUATIONS in TWO VARIABLES
A system of equations is a collection of two or more equations with the same set of unknowns. In solving a system of equations, we try to find values for each of the unknowns that will satisfy every equation in the system.
The equations in the system can be linear or non-linear. This tutorial
reviews systems of linear equations.
A problem can be expressed in narrative form or the problem can be expressed
in algebraic form.
Let's start with an example stated in narrative form. We'll convert it to an
equivalent equation in algebraic form, and then we will solve it.
Problem 2.1b:
An airplane flying into a head wind travels the 1800-mile flying distance
between two cities in 3 hours and 36 minutes. On the return flight, the same
distance is traveled in 3 hours. Find the ground speed of the plane and the
speed of the wind, assuming that both remain constant. [Ground speed is the speed of the plane if there were no wind.]
Answer: The ground speed of the plane is 550 miles per hour and the
wind speed is 50 miles per hour.
Solutions:
The relationship between distance, speed, and time is distance equals speed
times time. Let the symbol d represent distance, the symbol r represent
speed (or rate), and the symbol t represent the time. The relationship
between the three can then be expressed algebraically.
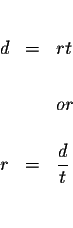
When the plane's speed is helped by the wind, the net speed increases and
the time to reach destination decreases. When the plane's is hindered by the
wind, the net speed decreases and the time to reach destination increases.
Therefore, we know that the plane had a tail wind when the time is 3 hours,
and the plane had a head wind when the time is 3 hours and 36
minutes.
Let's rewrite the problem.
With head wind: distance = (plane ground speed - wind speed) ![]() time or
time or
1,800= (plane speed - wind speed) ![]() 3 hours and 36
minutes
3 hours and 36
minutes
With tail wind: distance = (plane speed + wind speed) ![]() time
or
time
or
1,800= (plane speed + wind speed) ![]() 3 hours
3 hours
Let the symbol x represent the phrase plane ground speed and let
the symbol y represent the phrase wind speed, convert 3 hours and
36 minutes to 3.6 hours, and rewrite the two equations in algebraic form.
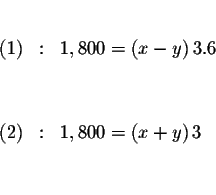
We have converted a narrative statement of the problem to an equivalent
algebraic statement of the problem. Let's solve this system of
equations.
A system of linear equations can be solved four different ways:
Substitution
Elimination
Matrices
Graphing
The Method of Substitution:
The method of substitution involves several steps:
Step 1:
Solve for x in equation (1).
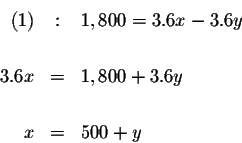
Step 2:
Substitute this value for x in equation (2). This will change equation (2)
to an equation with just one variable, y.
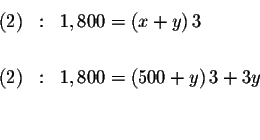
Step 3:
Solve for y in the translated equation (2).
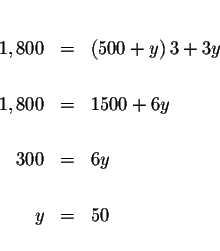
Step 4:
Substitute this value of y in equation (1) and solve for x.
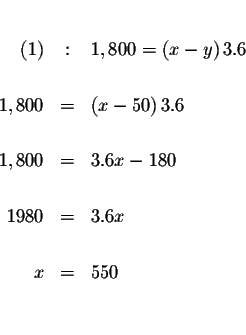
Step 5:
Check your answers by substituting the values of x and y in each of the
original equations. If, after the substitution, the left side of the
equation equals the right side of the equation, you know that your answers
are correct.

The process of substitution involves several steps:
In a two-variable problem rewrite the equations into equivalent forms so that when the equations
are added, one of the variables is eliminated, and then solve for the
remaining variable.
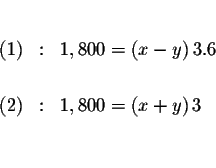
Multiply equation (1) by 3, multiply equation (2) by 3.6, and add the
two equations to form equation (3) with just one variable.
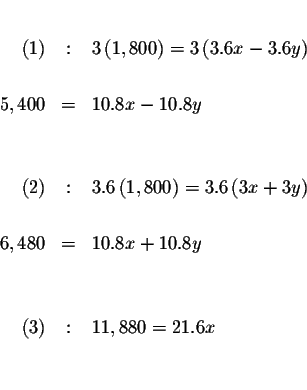
Solve for x.
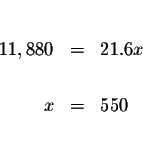
Substitute x=550 in equation (1) and solve for y.
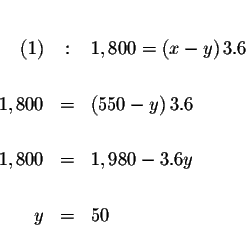
Check your answers.
The Method of Matrices:
This method is essentially a shortcut for the method of elimination.
Rewrite equations (1) and (2) without the variables and operators. The left
column contains the coefficients of the x's, the middle column contains
the coefficients of the y's, and the right column contains the
constants.
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrr...
... \\
& & & & \vert & & \\
3 & & 3 & & \vert & & 1,800
\end{array}
\right] $](img15.gif)
The objective is to reorganize the original matrix into one that looks like
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrr...
...
& & & & \vert & & \\
0 & & 1 & & \vert & & b
\end{array}
\right] \bigskip $](img16.gif)
Step 1.
Manipulate the matrix so that the number in cell 11 (row 1-col 1) is 1.
Multiply row 1 by
![]() to form a new row 1.
to form a new row 1.
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrr...
... \\
& & & & \vert & & \\
3 & & 3 & & \vert & & 1,800
\end{array}
\right] $](img18.gif)
Manipulate the matrix so that the number is cell 21 (row 2-col 1) is 0. Do
this by adding -3 times row 1 to row 2 to form a new row 2.
![\begin{eqnarray*}&& \\
-3\left[ Row\ 1\right] +\left[ row\ 2\right] &=&\left[ New\ Row\ 2\right] \\
&&
\end{eqnarray*}](img19.gif)
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrr...
...00 \\
& & & & \vert & & \\
0 & & 6 & & \vert & & 300
\end{array}
\right] $](img20.gif)
Manipulate the matrix so that the cell 22 is 1. Do this by multiplying row 2
by 1/6.
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrr...
...500 \\
& & & & \vert & & \\
0 & & 1 & & \vert & & 50
\end{array}
\right] $](img21.gif)
![\begin{eqnarray*}&& \\
\lbrack Row\ 2]+[Row\ 1] &=&[New\ Row\ 1] \\
&&
\end{eqnarray*}](img22.gif)
![$
\begin{array}{r}
(1) \\
\\
(2)
\end{array}
\left[
\begin{array}{rrrr...
...550 \\
& & & & \vert & & \\
0 & & 1 & & \vert & & 50
\end{array}
\right] $](img23.gif)
The method of Graphing:
In this method solve for y in each equation and graph both. The point of
intersection is the solution.
If you would like to go back to the problem page, click on Problem.
If you would like to review the solution to the next problem, click on Problem
If you would like to return to the beginning of the two by two system of equations, click on Example.
This site was built to accommodate the needs of students. The topics and problems are what
students ask for. We ask students to help in the editing so that future viewers will access
a cleaner site. If you feel that some of the material in this section is ambiguous or needs
more clarification, or if you find a mistake, please let us know by e-mail at sosmath.com.

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus