 SYSTEMS OF EQUATIONS in THREE VARIABLES
SYSTEMS OF EQUATIONS in THREE VARIABLES SYSTEMS OF EQUATIONS in THREE VARIABLES
SYSTEMS OF EQUATIONS in THREE VARIABLES
It is often desirable or even necessary to use more than one variable to model situations in many fields. We write and solve a system of equations in order to answer questions about the situation.
If a system of linear equations has at least one solution, it is
consistent. If the system has no solutions, it is inconsistent. If
the system has an infinity number of solutions, it is dependent.
Otherwise it is independent.
A linear equation in three variables is an equation equivalent to the
equation
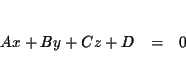
Example 7:
Solve the following system of equations for x, y and z:
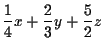 |
= | 20 | (1) |
| 3x-5y+2z | = | 11 | (2) |
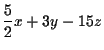 |
= | 7 | (3) |
1) Substitution,
2) Elimination
3) Matrices
SUBSTITUTION:
The process of substitution involves several steps:
Step 1: Let's get rid of the fractions. We can do this by multiplying
both sides of equation (1) by 12, and both sides of equation (3) by 2.
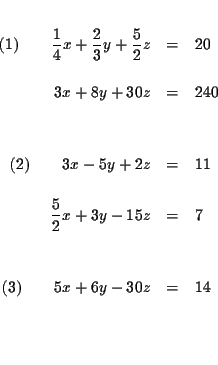
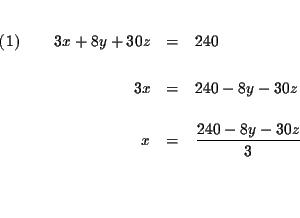
| = | 11 | ||
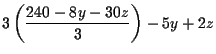 |
= | 11 | |
| = | 11 | ||
| -13y-28z | = | -229 | |
| 13y+28z | = | 229 | (4) |
| = | 14 | ||
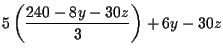 |
= | 14 | |
| = | 42 | ||
| 1,200-40y-150z+18y-90z | = | 42 | |
| -22y-240z | = | -1,158 | |
| 11y+120z | = | 579 | (5) |
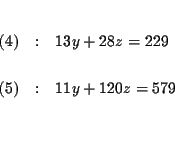
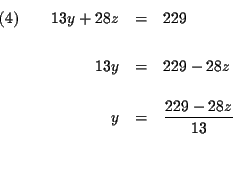
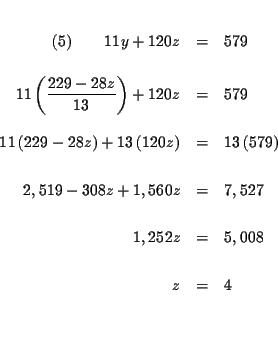
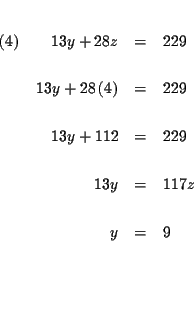
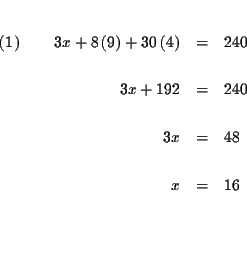
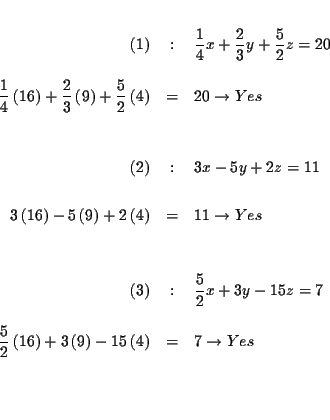
The process of elimination involves several steps: First you reduce three
equations to two equations with two variables, and then to one equation with
one variable.
Step 1: Decide which variable you will eliminate. It makes no
difference which one you choose. Let us eliminate z first.
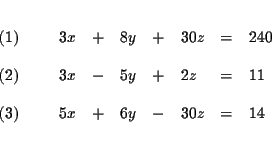
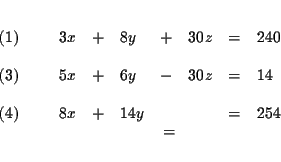
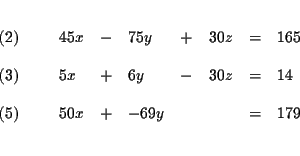
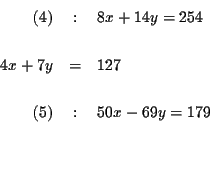
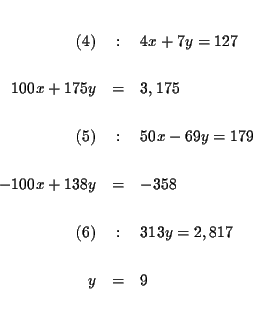
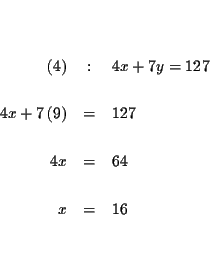
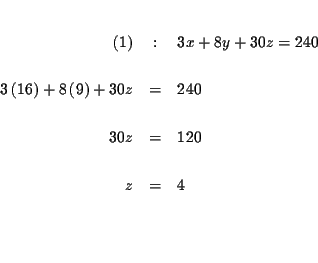
MATRICES:
The process of using matrices is essentially a shortcut of the process of
elimination. Each row of the matrix represents an equation and each column
represents coefficients of one of the variables.
Step 1:
Create a three-row by four-column matrix using coefficients and the constant
of each equation.
![\begin{eqnarray*}&& \\
&&
\begin{array}{r}
(1) \\
\\
(2) \\
\\
(3)
...
...\\
5 & & 6 & & -30 & \vert & 14
\end{array}
\right] \\
&&
\end{eqnarray*}](img27.gif)
The vertical lines in the matrix stands for the equal signs between both
sides of each equation. The first column contains the coefficients of x,
the second column contains the coefficients of y, the third column
contains the coefficients of z, and the last column contains the
constants.
We want to convert the original matrix
![\begin{eqnarray*}&& \\
&&
\begin{array}{r}
(1) \\
\\
(2) \\
\\
(3)
...
...\\
5 & & 6 & & -30 & \vert & 14
\end{array}
\right] \\
&&
\end{eqnarray*}](img27.gif)
![\begin{eqnarray*}&& \\
&&
\begin{array}{r}
(1) \\
\\
(2) \\
\\
(3)
...
... & \\
0 & & 0 & & 1 & \vert & c
\end{array}
\right] \\
&&
\end{eqnarray*}](img28.gif)
Step 2: We work with column 1 first. We would like the number 1 in
cell 11(Row1-Col 1). We can achieve this by multiplying Row 1 by
![]() .
.
![\begin{eqnarray*}&& \\
\frac{1}{3}\left[ Row\ 1\right] &=&\left[ New\ Row\ 1\right] \\
&&
\end{eqnarray*}](img30.gif)
![\begin{eqnarray*}&& \\
&&
\begin{array}{r}
(1) \\
\\
(2) \\
\\
(3)
...
...\\
5 & & 6 & & -30 & \vert & 14
\end{array}
\right] \\
&&
\end{eqnarray*}](img31.gif)
![\begin{eqnarray*}&& \\
-3\left[ Row\ 1\right] +\left[ Row\ 2\right] &=&\left[ ...
...ht] +\left[ Row\ 3\right] &=&\left[ New\ Row\ 3\right]
\\
&&
\end{eqnarray*}](img32.gif)
![\begin{eqnarray*}&& \\
&&
\begin{array}{r}
(1) \\
\\
(2) \\
\\
(3)
...
...rac{22}{3} & & -80 & \vert & -386
\end{array}
\right] \\
&&
\end{eqnarray*}](img33.gif)
![\begin{eqnarray*}&& \\
-\frac{1}{13}\left[ Row\ 2\right] &=&\left[ New\ Row\ 2\right] \\
&& \\
&&
\end{eqnarray*}](img35.gif)
![\begin{eqnarray*}&& \\
&&
\begin{array}{r}
(1) \\
\\
(2) \\
\\
(3)
...
...rac{22}{3} & & -80 & \vert & -386
\end{array}
\right] \\
&&
\end{eqnarray*}](img36.gif)
![\begin{eqnarray*}&& \\
-\dfrac{8}{3}\left[ Row\ 2\right] +\left[ Row\ 1\right]...
...ht] +\left[ Row\ 3\right] &=&\left[ New\ Row\
3\right] \\
&&
\end{eqnarray*}](img39.gif)
![\begin{eqnarray*}&& \\
&&
\begin{array}{r}
(1) \\
\\
(2) \\
\\
(3)
...
...}{39} & \vert & -\frac{10016}{39}
\end{array}
\right] \\
&&
\end{eqnarray*}](img40.gif)
![\begin{eqnarray*}&& \\
-\dfrac{39}{2504}\left[ Row\ 3\right] &=&\left[ New\ Row\ 3\right] \\
&&
\end{eqnarray*}](img42.gif)
![\begin{eqnarray*}&& \\
&&
\begin{array}{r}
(1) \\
\\
(2) \\
\\
(3)
...
...0 & & 0 & & 1 & \vert & 4
\end{array}
\right] \\
&& \\
&&
\end{eqnarray*}](img43.gif)
![\begin{eqnarray*}&& \\
-\dfrac{28}{13}\left[ Row\ 3\right] +\left[ Row\ 2\righ...
...ht] +\left[ Row\ 1\right] &=&\left[ New\
Row\ 1\right] \\
&&
\end{eqnarray*}](img46.gif)
![\begin{eqnarray*}&& \\
&&
\begin{array}{r}
(1) \\
\\
(2) \\
\\
(3)
...
...0 & & 0 & & 1 & \vert & 4
\end{array}
\right] \\
&& \\
&&
\end{eqnarray*}](img47.gif)
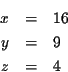
If you would like to test yourself by working some problem similar to this example, click on Problem.
This site was built to accommodate the needs of students. The topics and problems are what
students ask for. We ask students to help in the editing so that future viewers will access
a cleaner site. If you feel that some of the material in this section is ambiguous or needs
more clarification, or if you find a mistake, please let us know by e-mail at sosmath.com.

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus