 SOLVING EXPONENTIAL EQUATIONS - Example
SOLVING EXPONENTIAL EQUATIONS - Example
 SOLVING EXPONENTIAL EQUATIONS - Example
SOLVING EXPONENTIAL EQUATIONS - Example 
To solve an exponential equation, take the log of both sides, and
solve for the variable.

Example 7: Solve for x in the equation
![]()
Solution:
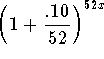 by dividing both sides by 500:
by dividing both sides by 500:
![]()
![]()
![]()
 :
:
![]()
is the exact answer and ![]() is the approximate answer.
is the approximate answer.
Check: Let's check the approximate answer with the original problem. When we substitute the above value of x in the left side of the equation, we get
![]()
You can also check your answer by graphing the function
![]()
and note where the graph crosses the x-axis. If you have worked the problem correctly, it should be the same value of x.
If you would like to review another example, click on Example.

 S.O.S MATHematics home page
S.O.S MATHematics home pageDo you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus