 SOLVING EXPONENTIAL EQUATIONS - Example
SOLVING EXPONENTIAL EQUATIONS - Example

To solve an exponential equation, take the log of both sides, and
solve for the variable.

Example 8: Solve for x in the equation
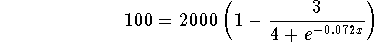
Solution:
-
- Step 1: Isolate the exponential term
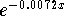 using steps 2 through 6.
using steps 2 through 6.
-
- Step 2: Divide both sides of the above equation by 2000:
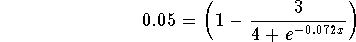
-
- Step 3: Subtract 1 from both sides of the above equation:
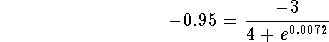
or
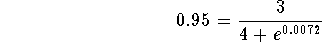
-
- Step 4: Multiply both sides of the above equation by
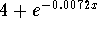 :
:
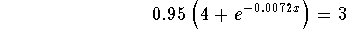
-
- Step 5: Divide both sides of the above equation by 0.95:
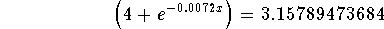
-
- Step 6: Subtract 4 from both sides of the above equation:
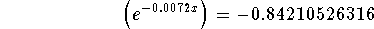
-
- Step 7: There is no way that the positive number e raised to a power will yield a negative number. There is no solution.
You could also graph the function
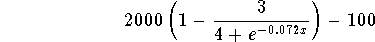
and note that the graph does not cross the x-axis. This means there is no
real solution.
If you would like to review another example, click on
Example.

[Previous Example]
[Next Example]
[Menu Back to Solving EE]
[Algebra]
[Trigonometry]
[Complex
Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Nancy
Marcus
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 SOLVING EXPONENTIAL EQUATIONS - Example
SOLVING EXPONENTIAL EQUATIONS - Example  SOLVING EXPONENTIAL EQUATIONS - Example
SOLVING EXPONENTIAL EQUATIONS - Example 

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page